5.9. Convergent Series
This section deals with real sequences of a special design, called series. Their members are calculated iteratively by summerizing given numbers. Although series are of course 'just' sequences,
they fill a special position: Their technical structure is needed for the introduction of a very important class of functions, the analytic functions.
Alone this part will provide three of them, namely the exponential function, the sine and the cosine.
|
Definition: If is any real sequence, the sequence
|
[5.9.1] |
is called the series respective to .
|
Consider:
We use 0 as inital value for technical reasons only. Especially the introduction of power series in part 11 will benefit from this.
Of course a sequence like is also called a series.
As the initial value k is readable from the series term itself we usually pass on noting down a series the very detailed way .
By definition each series is a sequence. However the reverse is also true, if we set
every sequence could be represented as a series:
|
|
[5.9.2] |
A series like the one in [5.9.2] is often called a telescoping series.
As series are special sequences all the properties achieved so far apply to series automatically!
It is just with the convergence property that we adjust the notation to match the new display format.
|
Definition and Notation: If the sequence is convergent we say that is a convergent series. We introduce a new symbol for the limit:
|
[5.9.3] |
|
In a first example we calculate the limit of the geometric series. We succeed using the summation formula in [5.2.4]and the convergence in [5.7.2].
For each q with the geometric series converges to
|
[5.9.4] |
This is an important result, often used in various contexts. Now we are able e.g. to prove exactly the perplexing identity :
This example shows a decimal expansion of the number 1, i.e. a digit representation with respect to the base 10. [5.9.4] now allows to prove for any natural number that every real number has a digit representation with respect to the base g, a so called g-adic representation.
|
Proposition (g-adic representation of real numbers): For a fixed base the set
is called the digit set of the g-adic system.
Now we have: For each there is a number and a sequence , such that
|
[5.9.5] |
We use the symbol
as an abbreviation for this expansion.
The ► Proof provides a constructive method to calculate the digit sequence.
|
Consider:
The example following [5.9.4] shows that we cannot prove the uniqueness of the representation in [5.9.5].
We use the classical symbols 0,1,2,3,4,5,6,7,8,9 to denote the members of the first ten digit sets, e.g.
for the dual system
for the decimal system
Other digit sets often use letters as further digit symbols. A common example is
-
for the hexadecimal system
Another example introduces a classical divergent series, the harmonic series.
|
Example:
- The harmonic series is divergent.
|
[5.9.6] |
Proof: It is impossible for to be a Cauchy sequence - and thus to be convergent -, because the following holds for all n:
|
All the results that we could establish for 'normal' real sequences are applicable to series as well.
There is for instance the Cauchy test
convergent is a Cauchy sequence
|
[5.9.7] |
which is often used when working with series. Other properties are more series specific like e.g. the very important convergence criteria in the latter part of this section.
Now we start with some simple properties, already however employing the Cauchy test.
|
Proposition:
- converges
converges.
|
[5.9.8] |
- converges
|
[5.9.9] |
Proof:
|
1. ►
|
For we see that
.
So we have: is a Cauchy sequence if and only if this true for , which proves our assertion according to [5.9.7].
|
|
2. ►
|
Take a given . As is a Cauchy sequence we find an such that
Specializing we thus get for all .
|
|
Consider:
[5.9.8] should be viewed as parallel to [5.4.10], but keep in mind that the limits normally would differ:
[5.9.9] is necessary for a series to be convergent. From example [5.9.6]
we see that this condition is not sufficient.
Another peculiarity comes with series having only positiv addends. Such a series is always an increasing sequence, so that a simple but effective criterion holds:
If is a sequence in we have
convergent bounded
|
[5.9.10] |
This behaviour in mind we introduce a second idea of convergence with our series.
|
Definition:
is said to converge absolutely, if the series
converges. |
[5.9.11]
|
|
The new concept is stronger than the old one: The next proposition shows that an absolutely convergent series is also convergent. On the other hand there are convergent series that don't converge absolutely.
A standard example is the alternating harmonic series.
|
Example: The alternating harmonic series
-
|
[5.9.12] |
is convergent, but not absolutely convergent.
Proof: We decompose the harmonic series into the sum of two convergent sequences. If we say for
we obviously have As teh sequences converges (to 0) according to the nesting theorem [5.5.8].
To prove the convergence of we note that the upper limit of summation is always odd. Thus all sequence members are of the kind
.
As all addends are positiv the sequence is increasing so that the convergence comes with the boundedness. We use the telescoping trick in [5.9.2] for that:
.
The series is the harmonic series, thus divergent due to [5.9.6].
|
|
Proposition: If converges absolutely then is convergent and the following inequality holds.
|
[5.9.13] |
Proof: We use the Cauchy test twice and employ the triangle inequality. As is a Cauchy sequence there is an for each such that
for all Thus is a Cauchy sequence as well and consequently convergent. To prove the estimate [5.9.13] we take the following inequality which holds for all sequence members:
With [5.5.2] we conclude . This is the assertion.
|
Testing series for convergence is often quite tricky, especially if we need to calculate the limit. There are however quite a few criteria, like the Cauchy test e.g.,
which can be used to prove at least the convergence. We now list the basic ones.
|
Proposition: Let and be two sequences and . Then we have the
-
boundedness test:
If is bounded then is convergent.
|
[5.9.14] |
-
comparison test:
If and if converges, so does .
|
[5.9.15] |
-
ratio test:
If then converges.
|
[5.9.16] |
-
root test:
If then converges.
|
[5.9.17] |
Proof:
|
1. ►
|
From we get the assertion is a direct consequence of [5.9.10].
|
|
2. ►
|
From the premise we see that all are positive. So the convergent sequence is increasing and we have
.
The assertion now is immediate with the boundedness test.
|
|
3. ►
|
We have due to the premise. an easy proof by induction guarantees for all i that
.
As the geometric series converges (c.f. [5.9.4]) we get the result from the comparison test.
|
|
4. ►
|
Again we succeed using the comparision test and the geometric series. Note that we get immediately from premise.
|
|
Consider:
The following example for the ratio test introduces three very important functions of calculus, the exponential function the sine and the cosine.
|
Example and Definition:
For every the series , and are convergent.
The function given by
|
[5.9.18] |
is called the exponential function.
-
The function given by
|
[5.9.19] |
is called the sine resp. the sine function.
-
The function given by
|
[5.9.20] |
is called the cosine resp. the cosine function.
Proof:
|
1. ►
|
There is nothing to do for . For we employ the ratio test [5.9.16] and to that end we choose a such that (note: is unbounded in ). Now we have for all :
.
Thus satisfies the ratio test (at least from k onwards).
|
|
2. ►
|
As the sine series converges according to the comparison test [5.9.14].
For the cosine series the same estimate holds and so its convergence is guaranteed as well.
|
|
Consider:
Calculating values is of course extremely difficult with these functions. The only exception is the value for 0
as all addends, except the first one, are equal to zero:
,
and
With the exponential function we are able to calculate a further value:
|
[5.9.21] |
Proof: We need to show (c.f. [5.7.7]):
.
-
With the generalized binomial theorem [5.2.5] we get the following estimate for all
We thus firstly know: .
-
Now let be fixed. For all we estimate from below as follows:
This inequlity remains valid for the limit as well. So that we have for all m:
.
From that we secondly get: .
With this new representation of Euler's number e we come back to two promises we made in 5.7:
-
-
We can approximate e much quicker than before using the sequence . Already
Furthermore to [5.9.21] the equality holds for all . [8.8.26] will show this.
The integral calculus will provide another access to the exponential function. It is there where we will go more deeply into the details.
|
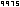 |
|